Key Takeaways:
If someone asks you, “How bright is that star?” and your answer is “Pretty bright,” that isn’t very useful. And, of course, it’s worthless for any type of comparative research. So for centuries, astronomers have used and refined a method of determining the brightness of stars and every other celestial object called the magnitude system.
Development
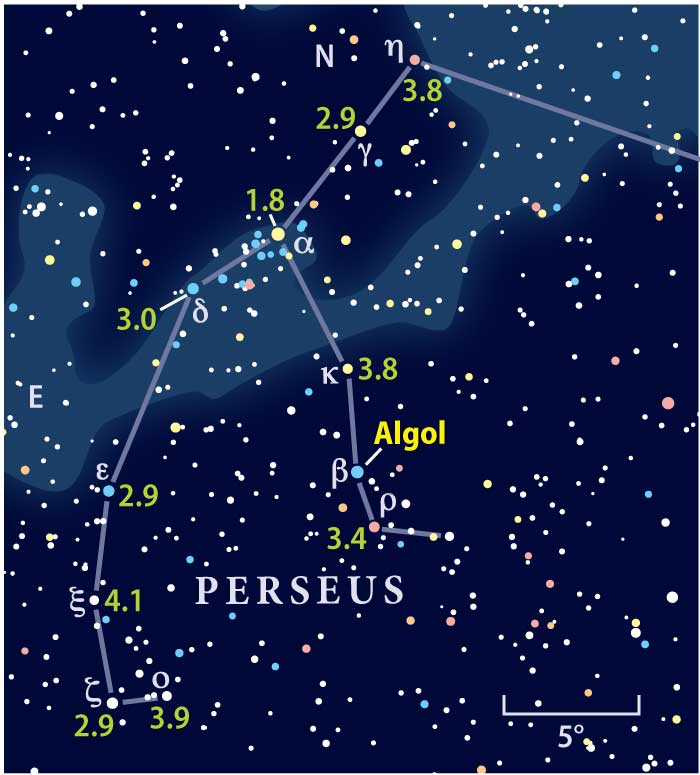
The first person known to catalog differences in star brightness was Greek astronomer Hipparchus, who lived in the second century b.c.e. He divided his listing of approximately 850 visible stars into six brightness ranges, calling the brightest stars “first magnitude.”
About 200 years later, the Egyptian polymath and author of the famous astronomy book Almagest, Claudius Ptolemy, refined the order of stars within these six levels. His catalog made clear that even within each magnitude range, some stars are brighter and some are dimmer. This system was used, almost unchanged, for more than 1,500 years.
In the 17th century, after the invention (and subsequent upgrading) of the telescope, Ptolemy’s system needed to be expanded. Using a telescope, people could see more stars than ever before. In fact, after Italian astronomer Galileo Galilei had constructed several telescopes, he added 7th-magnitude objects to his list of discoveries.
As time went on, astronomers not only discovered multitudes of faint stars, but they also needed a more precise way to compare brightnesses. By the end of the 18th century, another loose system had come into play. In it, the brightness difference of stars a single magnitude apart was roughly a ratio of 2.5.
In 1856, British astronomer Norman R. Pogson suggested that all observations be calibrated by using the constant 102/5. This defined the ratio between objects differing by one magnitude as 2.512, approximately, setting a mathematical standard that preserved Hipparchus’ original catalog system.
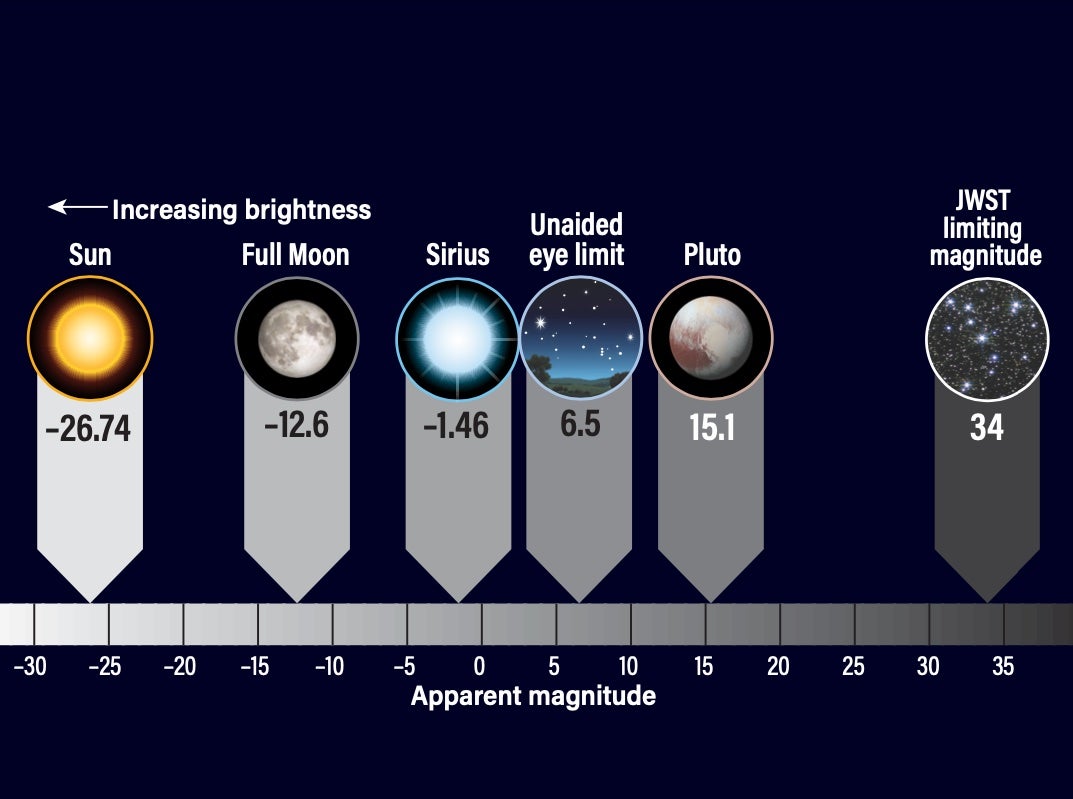
At this time, the concept of using magnitudes equal to and less than zero also appeared. The rationale was to keep one of the basics of the original system, where the limiting magnitude of the human eye is approximately 6th magnitude. With this limitation, and Pogson’s mathematical formula, it was evident that the three brightest stars, Sirius (Alpha [α] Canis Majoris), Canopus (Alpha Carinae), and Rigil Kentaurus (Alpha Centauri), were much brighter than 1st magnitude. And even brighter were the brightest planets, the Moon, and, of course, the Sun.
The number 2.512 is the fifth root of 100. This means that a difference of five magnitudes equals a 100-fold difference in brightness. As an example, Sirius, at magnitude –1.46, is roughly 100 times brighter than Wasat (Delta [Δ] Geminorum), which glows at magnitude 3.53.
How much brighter?
Observers often want to know how much brighter star A is than star B. For example, let’s find the brightness difference between Regulus [Alpha Leonis] at magnitude 1.4 and Delta Aurigae at magnitude 3.7. The formula to calculate this is simple: It is 2.512 raised to the power of the magnitude difference between the two stars. So, using this formula, we just need to calculate. 2.512(3.7 – 1.4). The difference between 3.7 and 1.4 is 2.3, so the formula becomes 2.5122.3 = 8.3. This tells us that Regulus is 8.3 times as bright as Delta Aurigae.
Adding magnitudes
There are times when you’d like to know the total magnitude of a double star. Pull out your calculator and use this formula to find the combined magnitude, which equals m₂ – 2.5log(10x + 1), where x = 0.4(m₂ – m₁) and m₁ and m₂ are the magnitudes of the stars. Our example here will be the popular double star Albireo (Beta [β] Cygni). The two stars have magnitudes of 3.2 and 5.1. So,
x = 0.4(5.1 – 3.2) = 0.76 and the formula becomes:
5.1 – 2.5log(100.76 + 1)
5.1 – 2.5log(6.754)
5.1 – 2.5(0.83)
which equals 3.026. Albireo’s total magnitude, then, is approximately 3.0.
Other systems
What I have described so far is just the visual apparent magnitude system. Apparent magnitude is how bright a star appears from Earth. The more scientific measurement, however, is absolute magnitude. Astronomers created this scale so they could compare the actual luminosities of stars to one another. The absolute magnitude of a star, then, is how bright it would be from a standardized distance of 10 parsecs (32.6 light-years).
In this system, the apparent magnitudes of stars nearer than 10 parsecs would be greater than their absolute magnitudes. For the vast majorities of stars, however, this is reversed. The Sun’s apparent magnitude is –26.7. Move it to a distance of 10 parsecs, and its absolute magnitude drops to 4.8. That is a brightness difference of 3.98 trillion!
Other systems use filters so astronomers can compare the light output of a single star in different wavelengths. One of the most useful is the UBV, also known as the Johnson-Morgan system, which provides a way to gauge the temperatures of stars. Three magnitudes are measured — through calibrated ultraviolet (U), blue (B), and visual (V) filters — and then compared. The visual filter is the measurement most often used when researchers talk about magnitude. The lower the number, the hotter the star, and vice versa.
Researchers even developed a system that considers all radiation a star emits, not just its light. Recording such a measurement finds a star’s bolometric magnitude, which helps determine the energy output from stars. For example, the Sun has a bolometric magnitude of 4.74, similar to its absolute magnitude.
The future is bright
Astronomers can now measure stellar brightness to a thousandth of a magnitude. We, as observers, don’t need that kind of precision. However, it’s nice to know that when you are plagued with the question, “How bright is it?”, you’ll actually know the answer.