Astronomy 101: Kepler’s laws

German astronomer Johannes Kepler was born in December 1571, and throughout his 59 years of life, he contributed immensely to science. He is most well-known, however, for his three laws of planetary motion. This work stemmed from a collaboration with Danish astronomer Tycho Brahe. Kepler mathematically analyzed some 20 years of precise planetary observations that Brahe collected. He determined how the solar system’s planets move the way they do and laid the foundation for Isaac Newton’s theory of gravity. What we now call his three laws are theories that are universal, verifiable, and precise — and they don’t just govern the motion of the planets, but also comets, asteroids, and other minor bodies orbiting the Sun.Kepler’s first law says that the orbit of every planet is an ellipse, with the Sun at one of two focus points. A circle is a special type of ellipse that has just one focus, which is located at its center. All other ellipses look like flattened circles, and have two focus points. If you take any point on the ellipse, the sum of the distances to the focus points is constant.

Before Kepler’s work, astronomers tried to describe the motion of the planets via interconnected circles, but they struggled to match observations. They also could not predict where planets would appear in the sky. Kepler’s theory changed that and showed how elegantly the planets moved.

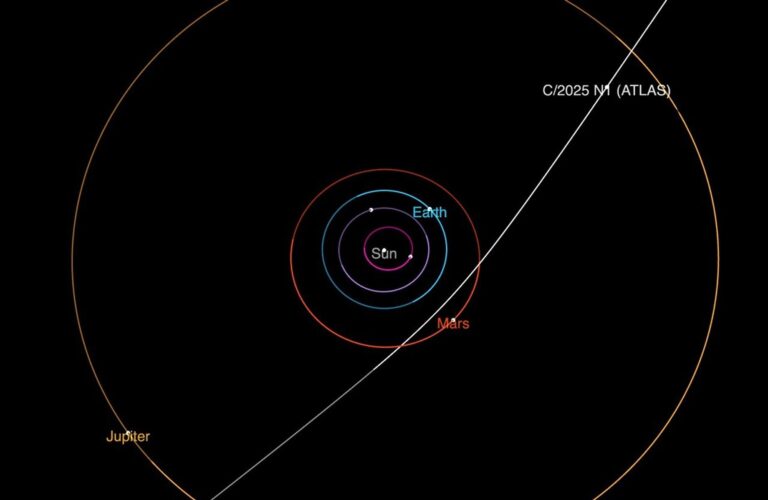
Kepler’s second law says that a line joining a planet and the Sun sweeps out equal areas during equal intervals of time. Thus, a planet moves fastest when it’s closest to the Sun (at a point called perihelion) and slowest at its farthest point from the Sun (known as aphelion). You can see this property best with objects that have longer elliptical orbits, like comets. As they near the Sun, they travel much faster than when they are more distant.

Nine years after Kepler published his first two laws, he determined the last one. Kepler’s third law says that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. The semi-major axis is just a term for half of the longest length of the ellipse. If you measure the period in Earth years and the orbit’s semi-major axis in astronomical units, the equation simplifies to period squared equals semi-major axis cubed. Astronomers use this relation to figure out the orbit of planets around other stars. They directly detect the world’s orbit period and can then figure out how far from the star the planet orbits.